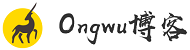树状数组
基本操作:1.快速求前缀和 2.修改一个数。
基本图示:
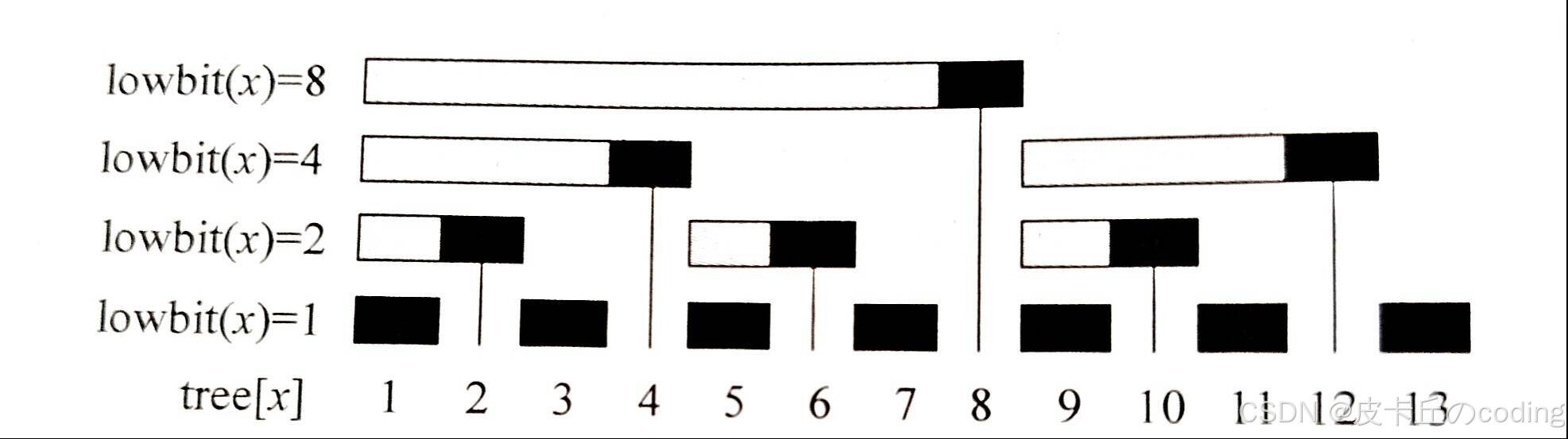
lowbit:求出一个数字二进制最后一个1的位置;
原理:
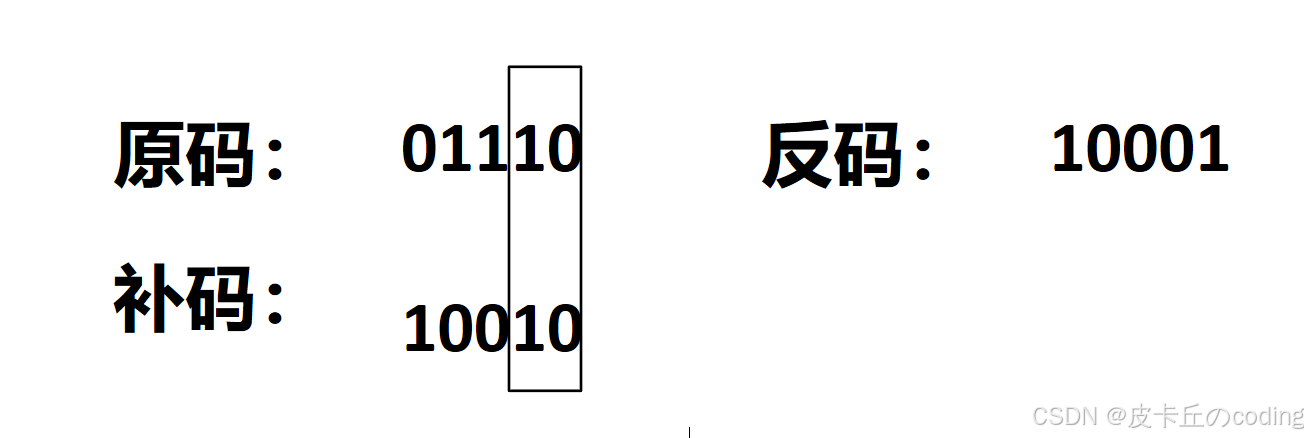
我们发现,除了最后一个1,以及其后面的0,其余位置都是反,则要求最后一位1的位置,可以将原码和补码按位&;而计算机中-x有取补码,则lowbit(x)=x&-x;
#define lowbit (x&(-x));
例子:数组:1,2,3,4,5,6,7
1.如果想要修改6=0110,
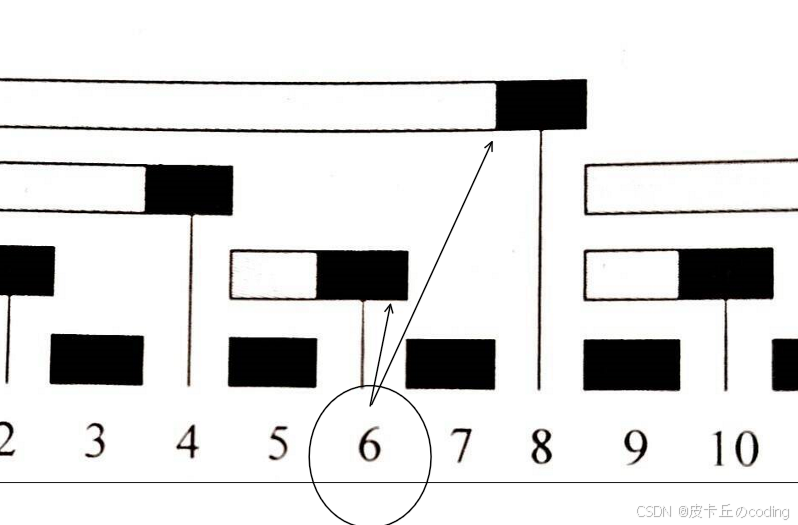
则会影响0110对应的:用lowbit+操作就可以修改,即6处修改,6+2(lowbit(6)=2)=8,对8处修改
2.如果想要查询【2,5】之间的和,可以求sum(5)-sum(1)
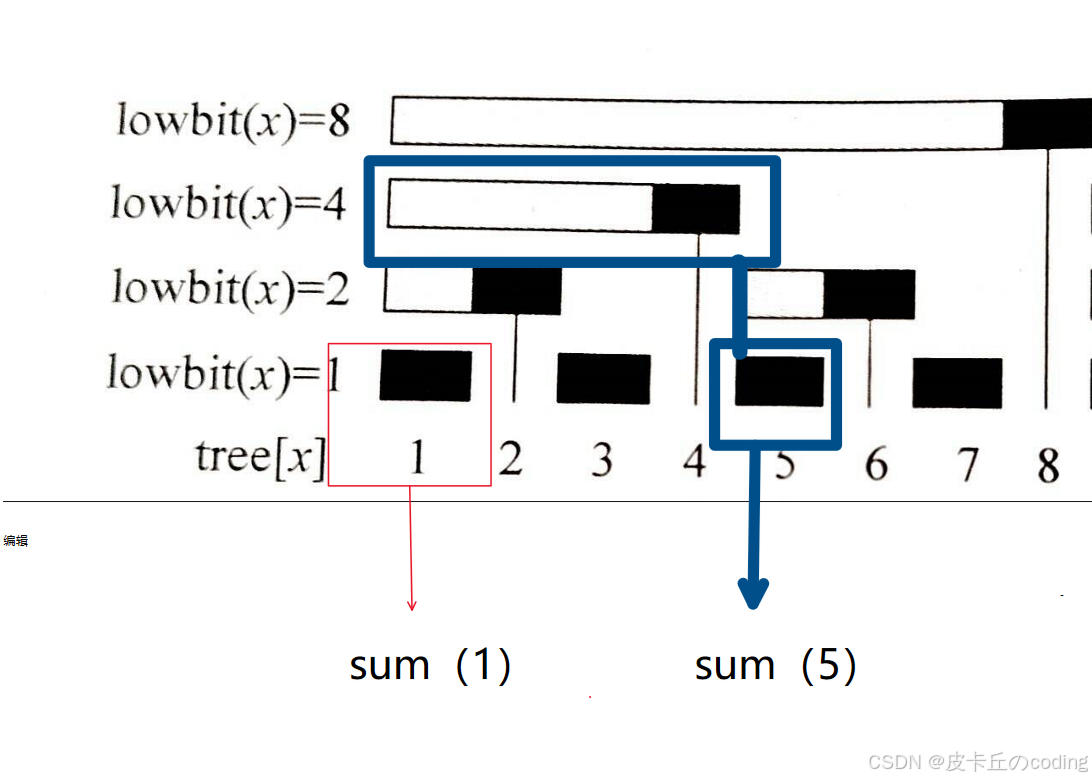
sum(5),5=0011,则用lowbit-就可以求出,sum加上5处的值,lowbit(5)=1,5-1=4,sum再加上4处的值,刚好就是sum(5),求出【2,5】,类似于前缀和,求出sum(5)-sum(1)。
综上所述:
void upload(int x,int d){
一个典型题:

我们不难知道,如果想要求解此题,想要知道V(题中)只要知道第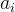 个数,左边有
个数,左边有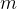 个比它大,右边有
个比它大,右边有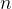 个比它大,然后
个比它大,然后 就是V的个数,
就是V的个数, 就是总的V图腾数,∧同理(左边,右边比它小)
就是总的V图腾数,∧同理(左边,右边比它小)
然后利用树状数组就可以求解逆序对:
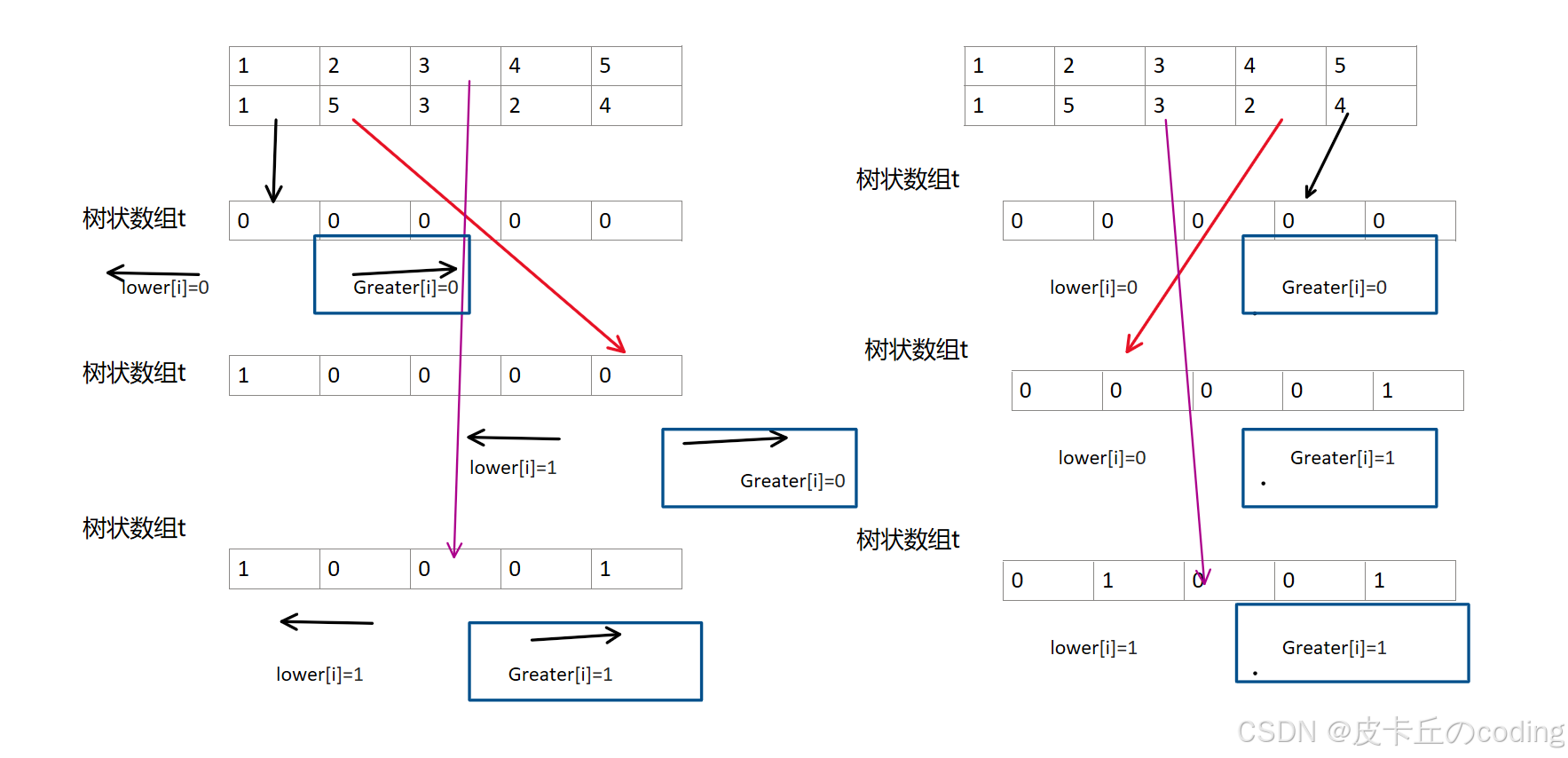
lower指比它大的数,Greater比它小的数。
第一遍求左边比它大(小)的数,第二遍(清空第一遍的tr,并逆序求一遍)求右边比它大(小)的数。
注:为啥会求出来,理由是每次更新树状数组, upload(y,1),则+1,之后遍历下一个数,就知道左边那群数比这个数大还是小的个数是多少(具体例子如下:)
Greater[i]=sum(n)-sum(y);
2: memset(tr, 0, sizeof tr);
for (int i = n; i; i -- )
res1+=great[i]*(LL)(sum(n)-sum(y));
res2+=lower[i]*(LL)(sum(y-1));
左边是第一次,右边是逆序第二次(上面代码1与代码2对应)
void upload(int x,int d){
int a[N],great[N],lower[N];
for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
great[i]=sum(n)-sum(y);//right
memset(tr, 0, sizeof tr);
for (int i = n; i; i -- )
res1+=great[i]*(LL)(sum(n)-sum(y));
res2+=lower[i]*(LL)(sum(y-1));
printf("%lld %lld\n", res1, res2);

利用差分数组:
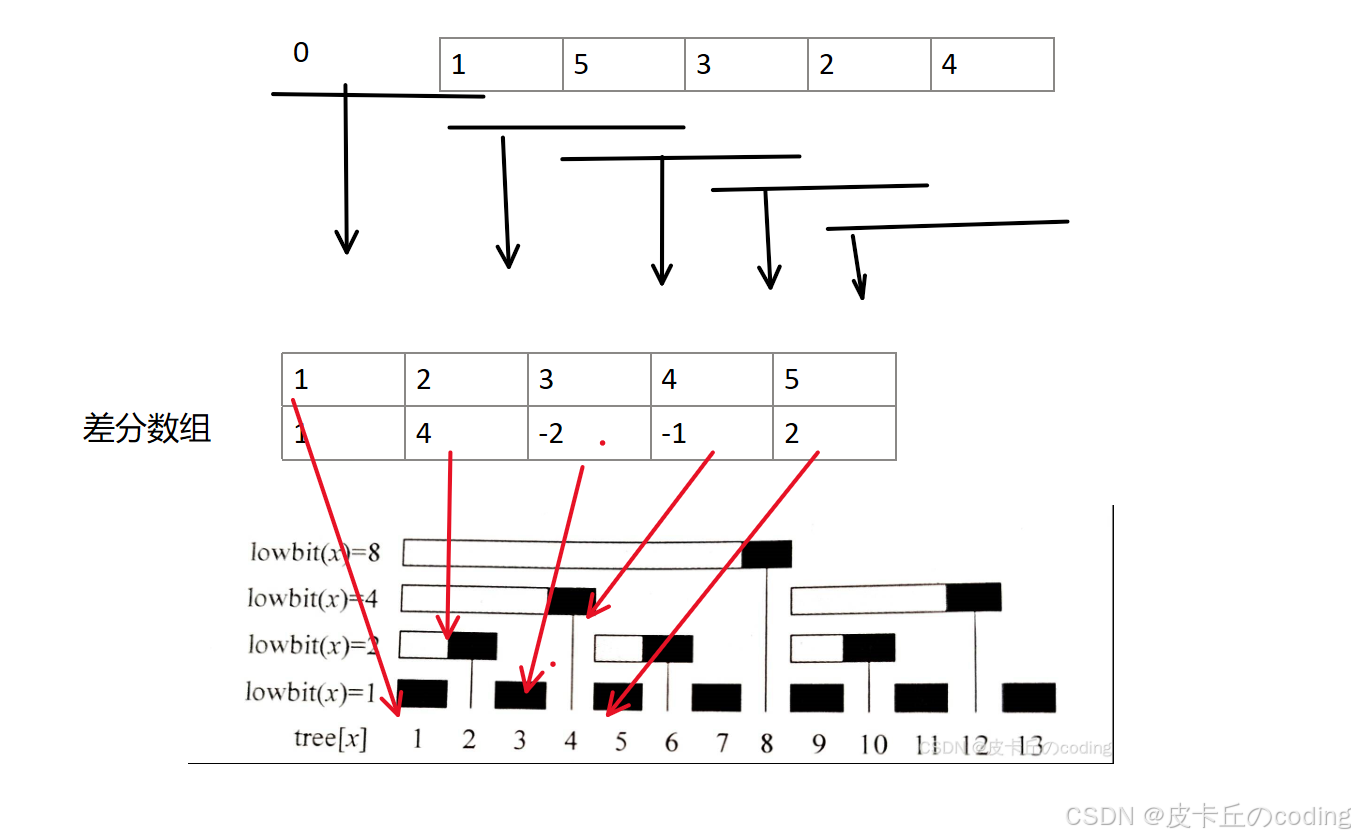
详见差分性质
void upload(int x,int d){
for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
for (int i = 1; i <= n; i ++ ) upload(i, a[i] - a[i - 1]);
upload(l, d), upload(r + 1, -d);
printf("%lld\n", sum(l));

1.记录差分
int b = a[i] - a[i -
1];
2.大致思路
如果要求区间修改,利用差分,同上。
但是,区间查询则需要利用一些数学推导:
其中,a为原数组,b为差分数组:
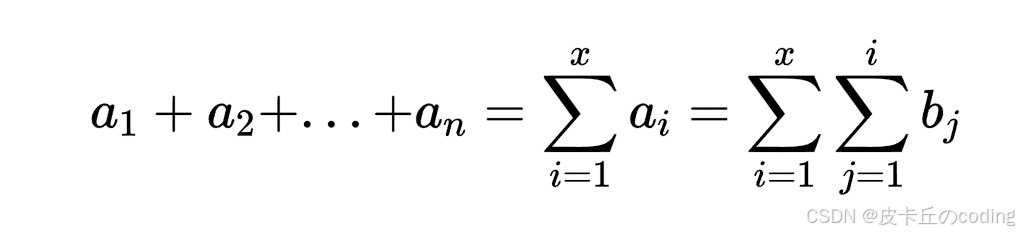
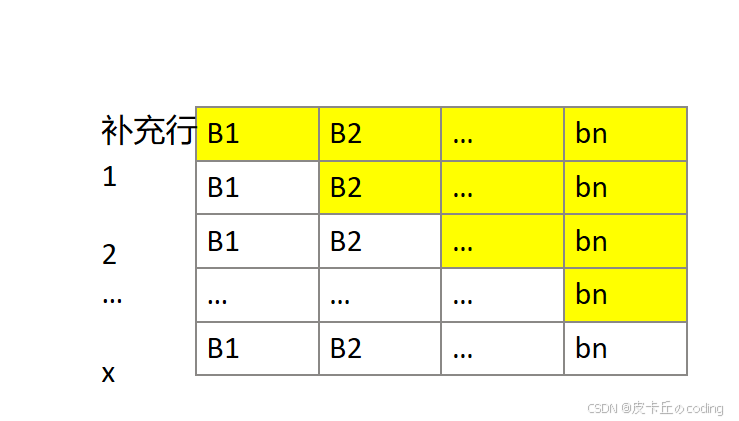
总面积: ,减去黄色部分:
,减去黄色部分: ,则白色区域:
,则白色区域:
return sum(tr1, x) * (x + 1) - sum(tr2, x);
LL tr1[N]; // 维护b[i]的前缀和
LL tr2[N]; // 维护b[i] * i的前缀和
区间
查询:
prefix_sum(r)-
prefix_sum(l
-1))
区间修改:
add(tr1, l, d), add(tr2, l, l * d);
add(tr1, r + 1, -d), add(tr2, r + 1, (r + 1) * -d);
总代码:
LL tr2[N]; // 维护b[i] * i的前缀和
void add(LL tr[], int x, LL c)
for (int i = x; i <= n; i += lowbit(i)) tr[i] += c;
for (int i = x; i; i -= lowbit(i)) res += tr[i];
return sum(tr1, x) * (x + 1) - sum(tr2, x);
for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
scanf("%s%d%d", op, &l, &r);
printf("%lld\n",prefix_sum(r)-prefix_sum(l-1));
add(tr1, l, d), add(tr2, l, l * d);
add(tr1, r + 1, -d), add(tr2, r + 1, (r + 1) * -d);
5.应用:谜一样的牛

这个题从正序入手不容易,可以从逆序入手。如何入手,可以举个例子:
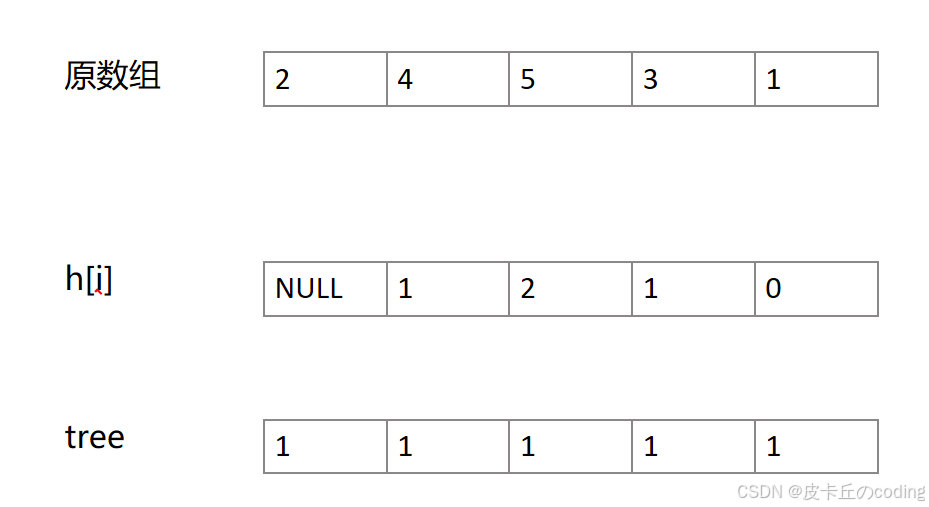
从h【4】=0开始,发现前面没有一个比它低,那么它最低,则是1。然后tree更新。
则发现,只要从最后一个开始,找到第h[i]+1个数就是它的位置,同时更新tree。
为了找到h[i]+1(其实就是求第k小的数,而tr数组记录了数组的前缀和,也就表示了数字到底是在数组中第几小),可以利用二分法。
void update(int x,int d){
for(int i=2;i<=n;i++) cin>>h[i];
for(int i=1;i<=n;i++) update(i,1);
for (int i = 1; i <= n; i ++ ) printf("%d\n", ans[i]);




个数,左边有
个比它大,右边有
个比它大,然后
就是V的个数,
就是总的V图腾数,∧同理(左边,右边比它小)






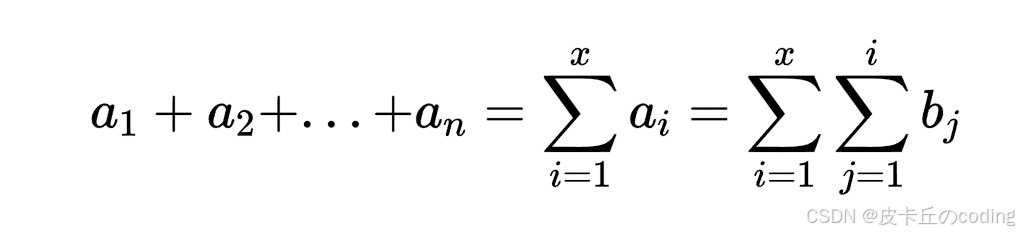

,减去黄色部分:
,则白色区域: