自带美感的贝塞尔曲线原理与实战——Android高级UI

时间2024-07-21 09:33:37发布ongwu分类云计算浏览75

这段代码绘制的效果和图中是一样的，我就不在贴图了。

2、三阶贝塞尔曲线

很幸运的是，三阶贝塞尔曲线在 Path 类中也有提供现成的 API

public void cubicTo(float x1, float y1, float x2, float y2, float x3, float y3)

我们借助上面三阶贝塞尔曲线静态图进行讲解。假设我们要绘制图中的这条红色的三阶贝塞尔曲线，只需进行如下代码操作

// 初始化路径对象

Path path = new Path();

// 移动至第一个控制点 A(ax,ay)

path.moveTo(ax, ay);

// 填充三阶贝塞尔曲线的另外三个控制点：

// B(bx,by) C(cx,cy) D(dx,dy) 切记顺序不能变

path.cubicTo(bx, by, cx, cy, dx, dy);

// 将贝塞尔曲线绘制至画布

canvas.drawPath(path, paint); 3、多阶贝塞尔曲线

看完二阶和三阶贝塞尔曲线的使用，是不是觉得非常的简单。但是系统提供的API就止步三阶贝塞尔曲线了，这是因为高阶在实际的开发过程中不是很常用，如果真的需要使用再高阶的贝塞尔曲线，那就只能自己进行降阶了。

我们借助以下的二阶贝塞尔曲线图来推导我们的降阶公式。先确定几个坐标 A(ax, ay)、B(bx, by)、C(cx, cy)、D(dx, dy)、E(ex, ey)、F(fx, fy)

当然一开始我们只知道 A、B、C 三个点的坐标，所以 D 的坐标由 A、B 进行求出具体如下

D点的x轴坐标：dx = ax + (bx-ax) * u = (1-u) * ax + u * bx (u ∈ [0,1])

D点的y轴坐标：dy = ay + (by-ay) * u = (1-u) * ay + u * by (u ∈ [0,1])

同理，E 的坐标由 B、C 进行求出，计算的逻辑完全一样。具体如下

E点的x轴坐标：ex = bx + (cx-bx) * u = (1-u) * bx + u * cx (u ∈ [0,1])

E点的y轴坐标：ey = by + (cy-by) * u = (1-u) * by + u * cy (u ∈ [0,1])

当得出 D和E 点，就可以进行求点F，逻辑还是一样。具体如下

F点的x轴坐标：fx = dx + (ex-dx) * u = (1-u) * dx + u * ex (u ∈ [0,1])

F点的y轴坐标：fy = dy + (ey-dy) * u = (1-u) * dy + u * ey (u ∈ [0,1])

至此最终的点 F 的可绘制坐标便得出。

推导公式

从以上的 计算公式 和之前的 “三个结论”，借助下图我们可以得出一个公式

P0k = (1-u) * P0k-1 + u * P1k-1

TIPs: x轴和 y轴的坐标计算公式是一样，所以我们这里就使用 x轴作为代表，方便讲解

由通用公式，想必童鞋们已经想到算法中的一个词叫 “递归”，的确没错，但细想一下还缺少一个 递归的终止条件 。我们再细想一下，其实终止条件就是 降阶最开始依赖的控制点是固定不变的，或是说是我们程序猿给定的，所以不用计算直接返回该控制点的x轴或y轴即可。

最终的递归公式如下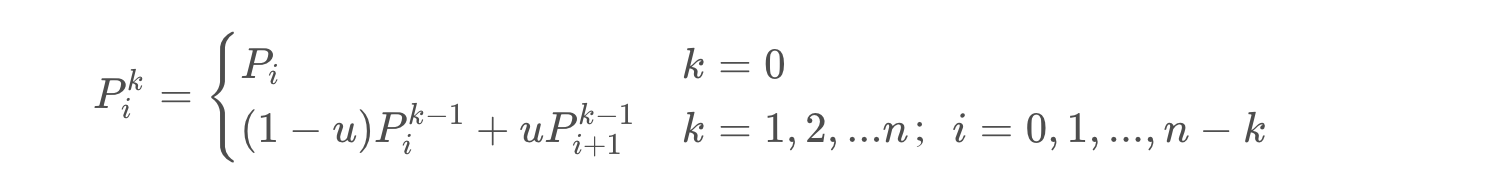

公式说明：

1、k 表示阶数，当 k=n 时，即相当于前面demo所讲的一阶控制点；当 k=0 时，表示最高阶的控制点，即我们程序猿最初给定的那几个控制点；

2、 i 表示点的下标，这个只是为了便于区分，可参照上面的图进行带入理解；

3、u 表示比例值

将通用公式编写成如下代码，调用 buildBezierPoint 方法，即可获得对应的最终的贝塞尔曲线，二阶和三阶也同样适用。

/**

构建贝塞尔曲线，具体点数由参数frame 决定@param controlPointList 控制点的坐标@param frame 帧数@return

public static List buildBezierPoint(List controlPointList,

int frame) {

List pointList = new ArrayList<>();

// 此处注意，要用1f，否则得出结果为0

float delta = 1f / frame;

// 阶数，阶数=绘制点数-1

int order = controlPointList.size() - 1;

// 循环递增

for (float u = 0; u <= 1; u += delta) {

pointList.add(new PointF(BezierUtils.calculatePointCoordinate(BezierUtils.X_TYPE, u, order, 0, controlPointList),

BezierUtils.calculatePointCoordinate(BezierUtils.Y_TYPE, u, order, 0, controlPointList)));

}

return pointList;

}

/**

计算坐标 [贝塞尔曲线的核心关键]@param type {@link #X_TYPE} 表示x轴的坐标， {@link #Y_TYPE} 表示y轴的坐标@param u 当前的比例@param k 阶数@param p 当前坐标（具体为 x轴或 y轴）@param controlPointList 控制点的坐标@return

public static float calculatePointCoordinate(@IntRange(from = X_TYPE, to = Y_TYPE) int type,

float u,

int k,

int p,

List controlPointList) {

/**

公式解说：（p表示坐标点，后面的数字只是区分）场景：有一条线p1到p2，p0在中间，求p0的坐标 p1◉--------○----------------◉p2 1 u p0 1 公式：p0 = p1+u*(p2-p1) 整理得出 p0 = (1-u)p1+up2

// 一阶贝塞尔，直接返回

if (k == 1) {

float p1;

float p2;

// 根据是 x轴还是 y轴进行赋值

if (type == X_TYPE) {

p1 = controlPointList.get§.x;

p2 = controlPointList.get(p + 1).x;

} else {

p1 = controlPointList.get§.y;

p2 = controlPointList.get(p + 1).y;

}

return (1 - u) * p1 + u * p2;

} else {

/**

这里应用了递归的思想：1阶贝塞尔曲线的端点依赖于 2阶贝塞尔曲线2阶贝塞尔曲线的端点依赖于 3阶贝塞尔曲线…n-1阶贝塞尔曲线的端点依赖于 n阶贝塞尔曲线1阶贝塞尔曲线则为真正的贝塞尔曲线存在的点

return (1 - u) * calculatePointCoordinate(type, u, k - 1, p, controlPointList) u * calculatePointCoordinate(type, u, k - 1, p + 1, controlPointList);

}

四、实战

经过漫长的理论，童鞋们早就摩拳搽掌，想用贝塞尔曲线前去挑战设计师，少侠勿急，看完实战我们再去碾压😄。

温馨提示：

理论是进阶中必不可少的部分，否则只知其然而不知其所以然。永远只能是作为使用别人代码的使用者，而不是创造者，更无法体会到创造的快乐。

贝塞尔曲线Demo的 Github 入口：传送门

1、圆变心

文章最开始出现的就是以下这张效果图，现在是时候进行撸起袖子开始打代码了。

效果图

动画分析：

动态图中，我们可以清楚的看出，从一个圆形慢慢变成心形，然后带有一点弹性效果。这样一分析，我们便需要三样东西：圆、心、弹性效果公式，接下来就是逐个突破。

准备零件

（1）圆 此圆非彼圆，我们不能借助canvas直接使用drawCircle进行绘制，因为这样的圆我们无法控制。那要如何处理呢？当然是用贝塞尔曲线画圆，因为这样一来这个 “圆”的控制点 就全都在我们的可控范围内，因为我持有了这些控制点就能进行坐标的变动，进而改变曲线的形状。

正当你在坐等这个 贝塞尔曲线画圆的公式 时，我又要泼一盆冷水了，因为根本就不存在这样一个公式。但我们可以通过前面的理论找到一个 近似圆的贝塞尔曲线公式 。

至于贝塞尔曲线为什么无法画出一个圆，有兴趣的童鞋们自行百度和google吧，毕竟这个一两行字无法解释清楚。

我们可以通过 三阶贝塞尔曲线 画出一段圆弧，通过四段圆弧就能拼凑出一个完整的圆了。但是又来了一个问题，三阶贝塞尔曲线有四个控制点，两端的控制点容易取，中间的控制点如何取？ 带着这个疑问，我们来看下面这个动画，当 控制点比例 从0到1增加过程中，蓝色区域从方形慢慢的变得接近圆，然后溢出变成圆角方形，红色的圆圈是用canvas的drawCircle绘制，从一些贝塞尔曲线绘制圆的论证资料和这里的动画效果可以得出，当 控制点比例等于0.55时(保留两位小数)，最接近一个圆。 前面提到的 四段圆弧的贝塞尔曲线 ，在这里使用了四种颜色，需要自己体验效果的童鞋，请进传送门。